第五集　　向量空间
我们可以对向量进行所谓“线性运算”，即通过加和（v+w）与数乘运算（3v）得到向量的线性组合。向量空间对线性运算封闭，即空间内向量进行线性运算得到的向量仍在空间之内。
包含于向量空间之内的一个向量空间称为原向量空间的一个子空间。
$R^{2}$ 中不穿过原点的直线就不是向量空间。子空间必须包含零向量，原因就是数乘0 的到的零向量必须处于子空间中。
$R^{2}$ 的子空间包括：
　　• $R^{2}$ 空间本身
　　• 过原点的一条直线（这是$R^{2}$空间中的一条直线，与$R^{1}$ 空间有区别）
　　• 原点 仅包含0 向量
$R^{3}$ 的子空间包括：
　　• $R^{3}$ 空间本身 3 维
　　• 过原点的一个平面 2 维
　　• 过原点的一条直线 1 维
　　• 原点 仅包含0 向量

第六集　　列空间和零空间　　
列空间
矩阵A 的列空间C(A)是其列向量的所有线性组合所构成的空间。
求解Ax=b 的问题，对于给定的矩阵A，对于任意的b 都能得到解么？

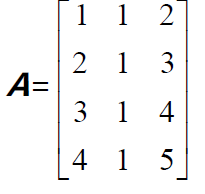
矩阵A 列向量的线性组合无法充满$R^{4}$，因此如果b不能被表示为A 列向量的线性组合时，方程是无解的。只有当b 在矩阵A 列空间C(A)里时，x 才有解。
而且，由于列向量不是线性无关的（第三个列向量为前两个列向量之和），所以尽管有3 个列向量，但是只有2 个对张成向量空间有贡献。矩阵A 的列空间为$R^{4}$ 内的一个二维子空间。

零空间
矩阵A 的零空间N(A)是指满足Ax=0 的所有解的集合。x 为含有3 个分量的向量，故矩阵A 的零空间是$R^{3}$ 的子空间。对于m*n 矩阵，列空间为$R^{m}$的子空间，零空间为$R^{n}$空间的子空间。
若方程变为

则其解集不能构成一个子空间。零向量并不在这个集合内。

对于列空间，它是由列向量进行线性组合张成的空间；而零空间是从方程组出发，通过让x 满足特定条件而得到的子空间。

第七集　　求解Ax=0：主变量，特解
计算零空间，矩阵A 的零空间即满足Ax=0 的所有x构成的向量空间。

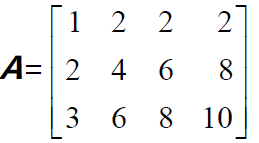
对于矩阵A 进行“行操作”并不会改变Ax=b 的解，因此也不会改变零空间（但是会改变列空间）。消元得到

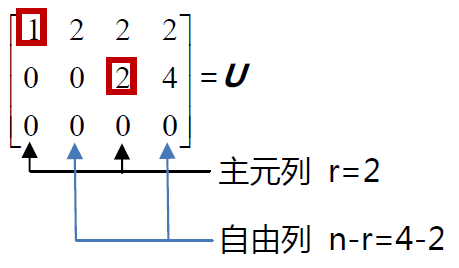
矩阵U 为梯形矩阵。其第三行变为零，是因为第三行的行向量本身就是第一行和第二行行向量的线性组合。矩阵的秩r就是矩阵的主元的个数，表示只有r个方程起作用。
当我们将系数矩阵变换为上三角阵U 时，就可以用回代求得方程Ux=0 的解。
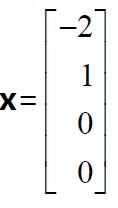
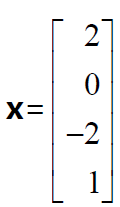
本例中，包含主元的矩阵第1 列和第3 列为主元列，而不包含主元的第2 列和第4列为自由列。对自由变量$x_{2}$和$x_{4}$我们可以进行赋值。例如令$x_{2}$=1，而$x_{4}$=0，可得一解，。取自由变量中$x_{2}$=0 而$x_{4}$=1，则可得到另一解，。
矩阵A 的零空间就是这些“特解”向量的线性组合所构成的向量空间，$x=C_{1}[-2,1,0,0]^{T} + C_{2}[2,0,-2,1]^{T}$。自由列的数目等于n-r，这是特解的数目和零空间的维数。

自由列可以表示为其左侧所有主元列的线性组合。

观察它的第五列自由列，其左侧有两个主元列，这两个主元列线性无关，第五列显然可以写成前两个主元列的线性组合。求Ux=0 的解，如果令其他所有自由列的x 分量都为0，而$x_{5}$=1，则方程变为：

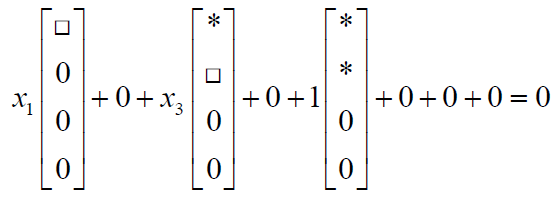
相当于求第五列如何用前两个主元列进行线性组合，所得解$x^{T}=[x1,0,x3,0,1,0,0,0]$即为原方程的特解之一。可知，四个自由变量分别取1 会得到零空间的四个特解。如果把自由变量都赋值为0 会求得0向量。

行最简阶梯矩阵
行最简阶梯矩阵形式R，其中主元为1，而主元列除主元外皆为0。

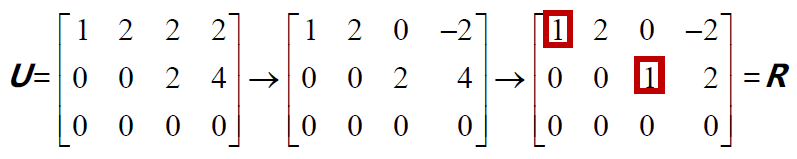
通过“列交换”，可以将矩阵R 中的主元列集中在左侧，从而在左上角形成这个单位阵。如果矩阵A 中的某些行是线性相关的，则在矩阵R 的下半部分就会出现一些完全为0的行向量。F即自由列消元后组成的部分。

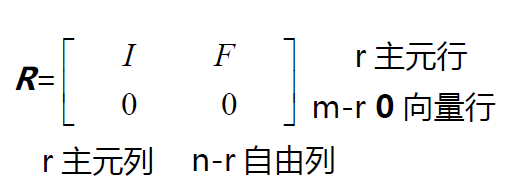
原方程Ax=0 变为Ux=0，又变为求解Rx=0。

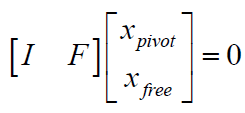
回代得$x_{pivot}=-Fx_{free}$，如果令$x_{free}=I$，则$x_{pivot}=-F$。所以零空间矩阵N最终形式为
，解x=CN（常数C）。
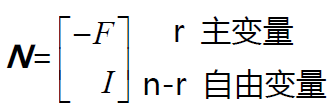
此时要注意如果在变换出R 左上角的单位阵的过程中采用了列交换，则最后的解要完成逆变换。在本例中，R进行了第二列和第三列交换才形成$\begin{bmatrix} I & F \end{bmatrix}$，所以零空间N=$\begin{bmatrix} -F\\ I \end{bmatrix}$,需要进行第二行和第三行交换，才能得到解$\begin{bmatrix} -2 & 2\\ 1& 0\\ 0& -2\\ 0& 1 \end{bmatrix}$。

第八集　　求解Ax=b：可解性和解的结构
可解的条件
取A为上一讲中的矩阵，则

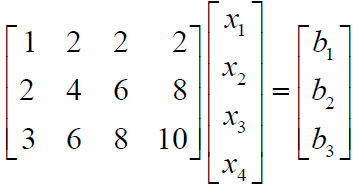
矩阵A 的第三行为第一行和第二行的加和，因此Ax=b 中b 的第3 个分量也要等于其第1 和第2 个分量的和，即只有当b 处于矩阵的列空间C(A)之中时，方程才有解。
对增广矩阵进行行消元，如下图所示。如果Ax=b 有解，则b3-b1-b2=0。

在本例中我们令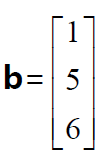
特解：求Ax=b 特解的方法是将自由变量均赋值为0，求解其主变量。令$x_{2}=x_{4}=0$得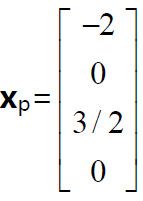

对于Ax=b的求解转变为Ux=c。此时四个主元列的线性组合可以组成任何$R^{4}$ 中的向量，我们将x中的自由变量赋值为0 就可以去掉自由列列向量的干扰，求得方程的特解$x_{p}$。

与零空间进行线性组合
Ax=b 的通解为$x_{complete}=x_{p}+x_{n}$，其中$x_{n}$为矩阵零空间中的一般向量。将$Ax_{p}=b$ 和$Ax_{n}=0$ 相加可得$A(x_{p}+x_{n})=b$。
上一讲我们得到了矩阵的零空间N(A)，因此方程Ax=的通解即为：

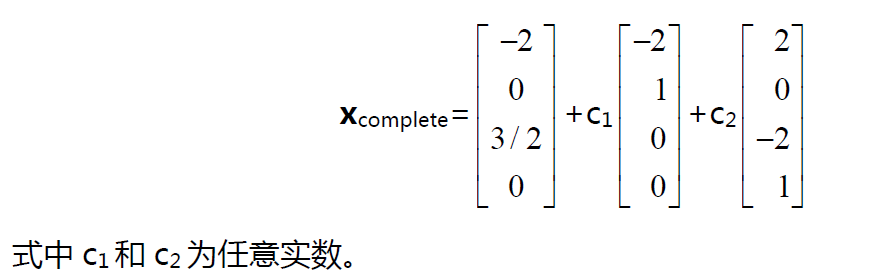
矩阵的零空间N(A)是$R^{4}$空间中的二维子空间，方程的解Ax=b 构成了穿过$x_{p}$点并和矩阵零空间平行的“平面“。但该”平面“并不是$R^{4}$空间的子空间。

前面求取Ax=b 的特解过程中，我们令所有自由变量赋值为0。如果不赋值为0，则等于带着自由列进行计算，但自由列其实也就是主元列的线性组合，这样求的特解$x_{p}’$只不过是$x_{p}$与零空间特解的一个加和。
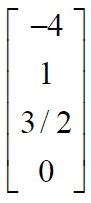
此例中若令$x_{2}=1,x_{4}=0$，则求特解$x_{p}’$=，而实际上$x_{p}’=x_{p}+x_{n1}$=。
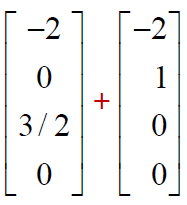
秩
矩阵的秩等于矩阵的主元数。如果m*n 矩阵的秩为r，则必有r<=m 且r<=n。列满秩：r=n，行满秩：r=m，满秩：r=m=n，矩阵可逆。m*n 给出了矩阵的尺寸，但是秩r 给出的是矩阵的实际“大小”。

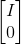
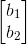
$r=n<m$情况下，$x$=时唯一解；$x$=时无解。

第九集　　线性无关，基和维数
线性无关
上一讲中$r=m<n$情况下，A 中具有至少一个自由变量，那么Ax=0 一定具有非零解。A 的列向量可以线性组合得到零向量，所以A 的列向量是线性相关的。

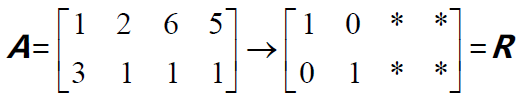
若$c_{1}x_{1}+c_{2}x_{2}+……+c_{n}x_{n}=0 仅在c_{1}=c_{2}=……=c_{n}=0$ 时才成立，则称向量$x_{1}，x_{2}……x_{n}$ 是线性无关的。若这些向量作为列向量构成矩阵A，则方程Ax=0 只有零解x=0。
在$R^{2}$ 中，两个向量只要不在一条直线上就是线性无关的。在$R^{3}$中，三个向量线性无关的条件是它们不在一个平面上（两个不共线向量形成一个平面，如果第三个向量不在这个平面上，则这三个向量张成$R^{3}$；如果第三个向量在这个平面上，则第三个向量与前两个向量线性相关）。

张成空间
当一个空间是由向量$v_{1}，v_{2}……v_{k}$的所有线性组合组成时，我们称这些向量张成了这个空间。如果向量$v_{1}，v_{2}……v_{k}$张成空间S，则S 是包含这些向量组合的最小空间。
基与维数
向量空间$R^{d}$的基是具有如下两个性质的一组向量$v_{1}，v_{2}……v_{d}$：
　　• $v_{1}，v_{2}……v_{d}$线性无关
　　• $v_{1}，v_{2}……v_{d}$张成该向量空间
所以$R^{n}$空间的每组基都包含n 个向量。
　　
2个向量，可以张成$R^{3}$中的一个平面，但是它们无法成为$R^{3}$空间的一组基。空间的每一组基都具有相同的向量数，这个数值就是空间的维数，比如以上例2个向量为基的空间维数是2。

列空间和零空间的基

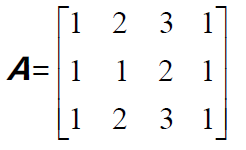
矩阵的秩r=矩阵主元列的数目=列空间的维数。比如前两列主元列组成了列空间C(A)的一组基。
零空间的维数=自由列的数目=n-r。本例中N(A)的维数为4-2=2。这两个特解就构成了零空间的一组基。
矩阵具有秩r 而没有维数dim，而空间有维数而没有秩。
　
第十集　　四个基本子空间　
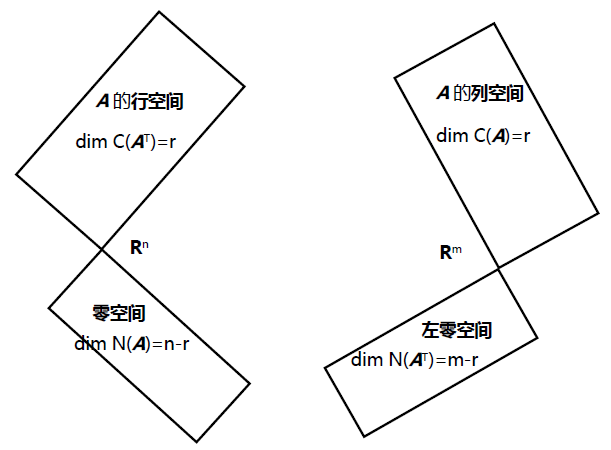
任意的m*n 矩阵A 都定义了四个子空间。
列空间 $C(A)$
矩阵A 的列空间是A 的列向量的线性组合在$R^{m}$空间中构成的子空间。
零空间$N(A)$
矩阵A 的零空间是Ax=0 的所有解x 在$R^{n}$空间中构成的子空间。
行空间$C(A^{T})$
矩阵A 的行空间是A 的行向量的线性组合在$R^{n}$空间中构成的子空间，也就是矩阵$A^{T}$的列空间。
左零空间$N(A^{T})$
我们称矩阵$A^{T}$的零空间为矩阵A 的左零空间，它是$R^{m}$空间中的子空间。

左零空间
矩阵$A^{T}$有m 列，而其秩为r，因此其自由列数目为m-r。所以dim $N(A^{T})$=m-r。
左零矩阵是满足$y^{T}A=0$的所有向量y 的集合。称之为左零矩阵是因为y出现在矩阵A左侧。

新向量空间
所有3*3 矩阵构成的集合是一个向量空间，符合对于线性运算封闭，称之为M。
M 的子空间包括：
　　• 所有的上三角阵
　　• 所有的对称阵
　　• 所有的对角阵
对角阵是前两个子空间的交集，其维数为3，具有以下一组基：

主元这个东西不是行变换消元得来的么，消元过程列空间不是已经改变了么，为什么所得出U 的主元数和主元列的位置还能够反映出矩阵A 列空间的状态呢？
因为初等行变换不会改变列向量的线性相关性。
把“秩”理解为行（列）向量中最大的线性无关向量组的向量数。在矩阵A 行变换消元成梯形阵后，很容易看到行空间内极大无关组之一就是主元所在的那前r 行，这r 个行向量可以张成行空间，因此行空间的维数与主元数相等都是r，并且前r行构成了行空间的一组基。

参考文献：
线性代数及其应用(美)David C.LayPDF
豆丁网MIT-线性代数笔记（上）